Question 111234: A box with an open top is to be constructed from a rectangular piece of cardboard with dimensions 5 in. by 10 in. by cutting out equal squares of side x at each corner and then folding up the sides as in the figure.
(a) Express the volume V of the box as a function of x, then determine the range and the domain of this function.
(b) Express the surface area S of the box as a function of x, then determine the range and the domain of this function.
(c) Find the value of x that gives the largest volume of the box
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Since you are cutting x out of each corner, the length of the box must be 10 - 2x, and the width of the box must be 5 - 2x, and the height is x. So the volume must be given by:
:

:
The domain of this function is determined by the physical limitations. In the first place, if x = 0, then there is no box, so one condition on the domain is that x > 0. On the other hand, if x = 2.5, there also is no box because the width (5 - 2x) would be zero, so the other condition on the domain is x < 2.5. So the entire expression for the domain is 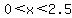 . .
:
For the range, on one end we know that the box must have some volume, so x > 0. On the other end, the maximum value of the range is equal to the maximum Volume. Therefore, we have to solve the third part of the problem now.
:
The volume function can be expressed as:

This function will have a local maximum at the point in the range where the first derivative is zero.
:







 , which is > 2.5, so invalid , which is > 2.5, so invalid
 , is the x coordinate of the local maximum , is the x coordinate of the local maximum
:

:
I'll let you simplify that mess, but it is the upper value of the range, and the answer to the third part of the problem.
:
Surface Area Problem:
:
The surface area of the flat piece of cardboard is 5 X 10 or 50 sq inches. But you are cutting out 4 pieces each x * x, so the box surface area is  . .
:
Again the domain must be 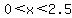 because if x is anywhere outside of that interval, there is no box. because if x is anywhere outside of that interval, there is no box.
:
The top end of the range is x < 50, and the bottom end is 25 which is the limit of S as x approaches 2.5.
|
|
|