Question 1112274: Three tennis balls, each of diameter 7cm, are sold in a cylindrical container. The internal diameter of the container is equal to the diameter of a tennis ball, and the height of the container is such that the tennis balls cannot move about. What fraction of the space within the container is occupied by the tennis balls?
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! Three tennis balls, each of diameter 7cm, are sold in a cylindrical container. The internal diameter of the container is equal to the diameter of a tennis ball, and the height of the container is such that the tennis balls cannot move about. What fraction of the space within the container is occupied by the tennis balls?
---------
find the volume of the cylinder.
find the volume of the 3 balls.
Subtract.
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The interesting fact is that the volume of the sphere is  of the volume of a smallest cylinder containing this sphere.
Archimedes, the great mathematician, physicist and engineer of the Ancient Greece, was the first who discovered it about 2200 years ago.
The last of the volume of a smallest cylinder containing this sphere.
Archimedes, the great mathematician, physicist and engineer of the Ancient Greece, was the first who discovered it about 2200 years ago.
The last  of the volume of this smallest cylinder is the volume of the cone inscribed to this cylinder.
Archimedes was so proud with this discovery, that these three solid bodies were placed on his grave in memory to his discovery. of the volume of this smallest cylinder is the volume of the cone inscribed to this cylinder.
Archimedes was so proud with this discovery, that these three solid bodies were placed on his grave in memory to his discovery.
The person who read it once in his life, will never forget it.
---------------
On Archimedes, read this Wikipedia article
https://en.wikipedia.org/wiki/Archimedes
Also, Archimedes gave an approximation of the value of  , showing that it is greater than , showing that it is greater than 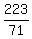 and less than and less than  . .
The day of  we celebrate today, March, 14 (3.14) ! we celebrate today, March, 14 (3.14) !
|
|
|