Question 1112231: Find the foci, eccentricity, length of latus rectum, and the x and y intercepts of the ellipse x^2/4 + y^2/16=1.
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website! For a wider-than-tall ellipse with center at ( , ), having vertices  units to either side of the center and foci  units to either side of the center, the ellipse equation is:
For a taller-than-wide ellipse with center at (,), having vertices units above and below the center and foci  units above and below the center, the ellipse equation is:
(y-h)^2/a^2 + (x-k)^2/b^2=1
The length of the semi-major axis is , a "semi-minor" axis is  , the length of the whole major axis is  ,the length of the whole minor axis is 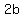 , and the distance between the foci is  .
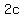The three letters , , and are related by the equation  .
you are given:
 or 
you also see that  ->  and  -> 
as you can see,  and  ; so, the center of your ellipse is at origin ( )
now we can find the foci, eccentricity, length of latus rectum, and the x and y intercepts:
center is at: (,  )
(, )
focus is the fixed value
(,) and (, )
use to find
 or 
so, foci is at:
(,  ) and (,  )
vertices at: (,  ) and (, )
(,  ) and (,  )
covertices at: (, ) and ( , )
( , ) and ( , )
eccentricity is denoted as 
which is
≈ 
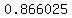
length of latus rectum:  => 
 -intercept: set 
 or 
-intercepts are at (, ) and (, )
 -intercept: set 
 or 
-intercepts are at (, ) and (, )
|
|
|
