SOLUTION: if low tide is 6 ft at 11 pm aturday night and high tide is 14 ft at 5 am sunday morning, write a function of the form h(t)=a sin b(t-h) + k that models the height of the tide t ho

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: if low tide is 6 ft at 11 pm aturday night and high tide is 14 ft at 5 am sunday morning, write a function of the form h(t)=a sin b(t-h) + k that models the height of the tide t ho      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1112227: if low tide is 6 ft at 11 pm aturday night and high tide is 14 ft at 5 am sunday morning, write a function of the form h(t)=a sin b(t-h) + k that models the height of the tide t hours after midnight (12 am sunday).
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
A function is requested to represent water level height 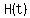H%28t%29 in feet,
as a function of t in hours after 12 AM Sunday,
1 hour after low tide at 11 PM Saturday,
and 5 hours before high tide at 5 AM Sunday.
The function must be of the form
H%28t%29=a%2Asin%28b%28t-h%29%29%2Bk .
The water level, 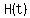H%28t%29 , ranges from 6ft to 14ft.
That means that the sinusoidal water level function h%28t%29
has an amplitude a (in feet) such that 2a=14-6=8
is the range around an average level (in feet) k=%2814%2B6%29%2F2=10 .
So, a=8%2F2=highlight%284%29 and highlight%28k=10%29 .
The time from low tide to high tide (in hours) is 6 ,
so the period of the function (in hours) is 2%2A6=12
(from low tide to next low tide).
That makes b=2pi%2F12 , and highlight%28b=pi%2F6%29 ,
so that when t (and t-h change by 12 ,
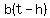b%28t-h%29 changes by 2pi .
After low tide, the water level will reach its average height
6%2F2=3 hours later at 2AM on Sunday, which is t=2 ,
and keep increasing.
So H%282%29=4sin%28%28pi%2F6%29%282-h%29%29%2B10=10 ,
4sin%28%28pi%2F6%29%282-h%29%29=0 ,
sin%28%28pi%2F6%29%282-h%29%29=0 .
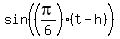If sin%28%28pi%2F6%29%28t-h%29%29 is increasing at t=2 ,
that means %28pi%2F6%29%282-h%29=0 or a multiple of 2pi .
From %28pi%2F6%29%282-h%29=0 , we get highlight%28h=2%29 as the simplest option.
Of course, h=2%2B12m for any integer m would also
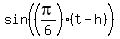make sin%28%28pi%2F6%29%282-h%29%29=0 , with sin%28%28pi%2F6%29%28t-h%29%29 increasing at t=2.
In sum, highlight%28H%28t%29=4sin%28%28pi%2F6%29%28t-2%29%29%2B10%29 .

CHECKING:
At 11 PM Saturday, t=-1 and
.
At 5 AM Sunday, t=5 and
.
The graph of y=4sin%28%28pi%2F6%29%28x-2%29%29%2B10 is