Question 1111884: A bus and truck left town A at 10:00 am and went along the road between towns A and B at a constant speed. At the same time, a car set off from B along the same road at a constant speed. The car first met the truck 30 minutes later and then after 10 more minutes, it met the bus. The truck reached B, immediately turned back, and on it's way to A, met the bus 2 hours since it left A. When will the truck get back to A?
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
A bus and truck left town A at 10:00 am and went along the road between towns A and B at a constant speed.
At the same time, a car set off from B along the same road at a constant speed.
The car first met the truck 30 minutes later and then after 10 more minutes, it met the bus.
The truck reached B, immediately turned back, and on it's way to A, met the bus 2 hours since it left A.
When will the truck get back to A?
~~~~~~~~~~~~~~~~~
First step is to translate the words into Math equations.
Let C = speed of the car (in units of length per MINUTE),
T = speed of the truck; B = speed of the bus (in the same units).
(1) The car first met the truck 30 minutes ====> 30*C + 30*T = D, the distance between A and B.
(2) Then after 10 more minutes, the car met the bus ====> 40*C + 40*B = D.
(3) The truck reached B, immediately turned back, and on it's way to A, met the bus 2 hours since it left A.
====> 120*T + 120*B = 2D.
Stretch your mind as strong as you can to understand all and each of these equations.
Thus the major part IS DONE - the setup is completed.
You have this system of equations
30*C + 30*T = D
40*C + 40*B = D
120*T + 120*B = 2D.
Or, equivalently
120*C + 120*T = 4D (1)
120*C + 120*B = 3D (2)
120*T + 120*B = 2D. (3)
Add all three equations (1), (2) and (3)
240C + 240T + 240B = 9D. (4)
Divide by 2 both sides of (4) to get
120C + 120T + 120B = 4.5D (5)
Subtract eq(2) from (5) (both sides). You will get
120T = 4.5D - 3D = 1.5D ====> D/T = 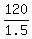 = 80.
It means that the truck needs 80 minutes to cover the distance between A and B.
In the problem, the truck covers the distance D twice.
It requires 2*80 = 160 minutes = 2 hours and 40 minutes
It is time for the truck to be on the way.
When will the truck get back to A ? - at 10:00 am + 2 hours and 40 minutes = 12:40, or 40 minutes after noon.
***********************
* * * S O L V E D * * *
***********************
|
|
|
