Question 1111883: A student rows at a constant speed (relative to the water) downstream in the Nambucca River from Bowraville to Macksville, which takes 3 hours, and back upstream in 4 hours. If the river flows at a constant rate, find the number of hours it would take a piece of driftwood to float downstream from Bowraville to Macksville.
Answer by ikleyn(52813)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let L be the distance between the cities (in some units, miles or kilometers - IT DOES NOT MATTER, as you will see further).
Let u be the speed of the boat in still water (in the CORRESPONDING units), and
let v be the rate of the current (in the same units).
You are given
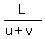 = 3 hours (1) (rowing downstream) = 3 hours (1) (rowing downstream)
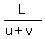 = 4 hours (2) (rowing upstream)
From these equations
3*(u+v) = L (1')
4*(u-v) = L (2')
or, equivalently
3u + 3v = L {1'')
4u - 4v = L (2'')
What I need is to find the ratio = 4 hours (2) (rowing upstream)
From these equations
3*(u+v) = L (1')
4*(u-v) = L (2')
or, equivalently
3u + 3v = L {1'')
4u - 4v = L (2'')
What I need is to find the ratio 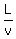 . It is EXACTLY the time a piece of driftwood to float downstream from Bowraville to Macksville,
which is under the question.
For it, I am going to eliminate the variable "u" from the equations (1'') and (2'') and to express "v" via L (or, conversely, express L via "v").
So I multiply eq(1'') by 4 (both sides) and multiply eq(2'') by 3 (both sides). I will get
12u - 12v = 3L (3)
12u + 12v = 4L (4)
Now subtract eq(3) from eq(4). You will get
24v = L, which implies . It is EXACTLY the time a piece of driftwood to float downstream from Bowraville to Macksville,
which is under the question.
For it, I am going to eliminate the variable "u" from the equations (1'') and (2'') and to express "v" via L (or, conversely, express L via "v").
So I multiply eq(1'') by 4 (both sides) and multiply eq(2'') by 3 (both sides). I will get
12u - 12v = 3L (3)
12u + 12v = 4L (4)
Now subtract eq(3) from eq(4). You will get
24v = L, which implies 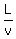 = 24.
It gives the ANSWER: it will take 24 hours for a piece of driftwood to float downstream from Bowraville to Macksville
(since this piece moves with the rate of the current). = 24.
It gives the ANSWER: it will take 24 hours for a piece of driftwood to float downstream from Bowraville to Macksville
(since this piece moves with the rate of the current).
Solved.
-----------------
It is a CLASSIC "downstream-upstream" problem.
See the lesson
- Unpowered raft floating downstream along a river
in this site.
You can find many other fully solved problems on upstream and downstream round trips with detailed solutions in lessons
- Wind and Current problems
- More problems on upstream and downstream round trips
- Wind and Current problems solvable by quadratic equations
- Unpowered raft floating downstream along a river (*)
- Selected problems from the archive on the boat floating Upstream and Downstream
in this site.
Read them attentively and learn how to solve this type of problems once and for all.
The relevant lesson is marked (*) in this list.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|