Question 111173: Connie McNair's boat goes 12 mph. Find the rate of the current of the river if she can go 6 mi upstream in the same amount of time she can go 10 mi downstream.
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! The basic formula you need to use here is  where d is distance, r is rate (or speed), and t is time.
:
Let's say the rate of the current is 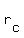 . When the boat is going upstream, against the current, the actual speed of the boat is 12mph MINUS the rate of the current, and when it is going downstream, the actual speed is 12 PLUS the rate of the current.:
:
if , then  . So, her time going upstream is:
:
Likewise, her time going downstream is:
:
but the problem states that the time spent going upstream is the same as the time going downstream, so we can set the right sides of the two equations above to be equal:
:
Remembering that if  , then  , we can write:
:
:
so the rate of the current is 3 mph.
|
|
|
