|
Question 1111648: A certain amount of money is invested at 6% per year. A second amount is Php5000 larger than the first is invested at 8% per year. The interest from the investment at the higher rate exceeds the income from the lower investment by Php500. Find the investment at each rate.
Found 3 solutions by Theo, ikleyn, TeachMath:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! x equals the amount invested at 6%.
x + 1000 equals the amount invested at 8%.
the interest on the amount invested at 8% is 500 more than the interest on the amount invested at 6%.
the equation for that is:
.08 * (x + 1000) = .06 * x + 500
simplify to get .08 * x + 80 = .06 * x + 500
subtract .06 * x from both sides of this equation and subtract 80 from both sides of this equation to get:
.02 * x = 420
divide both sides of this equation by .02 to get:
x = 420 / .02 = 21,000
go back to your original equation and replace x with 21,000.
the original equation is .08 * (x + 1000) = .06 * x + 500
replace x with 21,000 to get:
.08 * 22,000) = .06 * 21,000 + 500
simplify to get:
1,760 = 1,760, which is true.
.08 * 22,000 = 1,760
.06 * 21,000 = 1,260
the difference is 500, as stated in the problem statement.
the solution is:
21,000 was invested at 6% and 22,000 was invested at 8%.
Answer by ikleyn(52855)  (Show Source):
You can put this solution on YOUR website! .
A certain amount of money is invested at 6% per year. A second amount is Php5000 larger than the first is invested at 8% per year.
The interest from the investment at the higher rate exceeds the income from the lower investment by Php500. Find the investment at each rate.
~~~~~~~~~~~~~~~~~~~~~~~~~
Interest - interest = 500.
0.08*(x+5000) - 0.06x = 500 (<<<---=== x = the smaller amount at 6%)
0.08x + 400 - 0.06x = 500
0.02x = 500 - 400 = 100 + x = 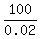 =  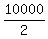= 5000.
Answer. Php 5000 was invested at 6% and Php 10000 was invested at 8%.
Check. 0.08*10000 - 0.06*5000 = 500 Php. ! Correct !
Solved.
---------------
Any other answer is I N C O R R E C T.
=================
To see many other similar solved problems on investment, look into the lesson
- Using systems of equations to solve problems on investment
in this site.
You will find there different approaches (using one equation or a system of two equations in two unknowns), as well as
different methods of solution to the equations (Substitution, Elimination).
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic "Systems of two linear equations in two unknowns".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by TeachMath(96)  (Show Source):
|
|
|
| |
