SOLUTION: For x and y positive integers, if xy > = 9, what is the smallest possible sum of x + y?

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: For x and y positive integers, if xy > = 9, what is the smallest possible sum of x + y?      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1111386: For x and y positive integers, if xy > = 9, what is the smallest possible sum of x + y?
Answer by ikleyn(52790) About Me  (Show Source):
You can put this solution on YOUR website!
.
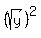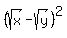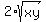x + y = %28sqrt%28x%29%29%5E2 + %28sqrt%28y%29%29%5E2 = %28sqrt%28x%29+-+sqrt%28y%29%29%5E2 + 2%2Asqrt%28xy%29.


This line is an IDENTITY.


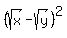Now, the term  %28sqrt%28x%29+-+sqrt%28y%29%29%5E2  is ALWAYS positive (non-negative), therefore, we can continue and transform this line / identity in THIS WAY


x + y = 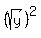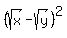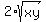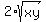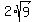%28sqrt%28x%29%29%5E2 + %28sqrt%28y%29%29%5E2 = %28sqrt%28x%29+-+sqrt%28y%29%29%5E2 + 2%2Asqrt%28xy%29  > =  2%2Asqrt%28xy%29 = 2%2Asqrt%289%29 = 2*3 = 6.


Thus we have established this inequality


x + y >= 6.


Taking x= y= 3,  we get the exact value  of 6  for  x+y.  


In all other cases we have inequality  x + y > 6.


So, under the given condition  xy >= 9,  the smallest value for  x + y  is  6.

SOLVED.