Question 1111302: A ball is thrown vertically upward with an initial velocity of 4848 feet per second. The distance s (in feet) of the ball from the ground after t seconds is s equals 48 t minus 16 t squareds=48t−16t2.
(a) At what time t will the ball strike the ground?
(b) For what time t is the ball more than 2020 feet above the ground?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are typos in this problem.
The initial velocity must have been 48 feet per second,
and part (b) should ask for how long the ball is more than 20 feet above the ground.
On planet Earth, if the height in feet,  , of a ball , of a ball
 seconds after it was thrown upwards is seconds after it was thrown upwards is
 , ,
then the ball was launched upwards from ground level,
and with an initial upwards velocity of  ft/s. ft/s.
Also, that ball would reach a maximum height of only 36 ft.
(a) A ball whose height above the ground is given by
 , with , with  in seconds, in seconds,
is at a height  (meaning on the ground) (meaning on the ground)
when  . .
So, to know the value of  when that happens, we have to solve when that happens, we have to solve


So, the ball was at ground level at  , ,
and when  , which means , which means  . .
In other words, the ball is launched up from ground level at  , ,
and is back on the ground at  , ,
hitting the ground  after it was thrown vertically upward. after it was thrown vertically upward.
(b) The ball reaches maximum height halfway during its flight,
at  , and we can calculate that for , and we can calculate that for  , ,  . .
At some time  , ,
between being thrown upwards and reaching maximum height at  , ,
the ball is at a height of 20 feet,  , and still going up. , and still going up.
After reaching maximum height, the ball is falling towards the ground,
and at some time  during that fall it will be at a height of 20 ft, with during that fall it will be at a height of 20 ft, with  again. again.
To find  and and  we have to solve for we have to solve for  when when  . .
We have to solve  : :


 (dividing by 4 both sides of the equal sign) (dividing by 4 both sides of the equal sign)
That simpler quadratic equation can be solved by factoring 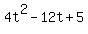 to get to get
 so that so that
either   
or    . .
Like all quadratic equations,
 can also be solve can also be solve
by applying the quadratic formula,
or by "completing the square."
|
|
|