SOLUTION: {{{ 2^(x+1)+2^x=3^(y+2)-3^y }}}, x, y ∈ Z. Find x.

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: {{{ 2^(x+1)+2^x=3^(y+2)-3^y }}}, x, y ∈ Z. Find x.      Log On


   

Question 1111149: +2%5E%28x%2B1%29%2B2%5Ex=3%5E%28y%2B2%29-3%5Ey+, x, y ∈ Z. Find x.
Answer by ikleyn(52798) About Me  (Show Source):
You can put this solution on YOUR website!
.
One solution is  x = 3,  y = 1.


Then your equation takes the form


2^4 + 2^3 = 3^3 - 3^1,    and it is true, because each side is equal to 24.



    Next statement is that  there is NO any other solution.



You can easily prove it on your own, based on this notices:


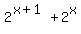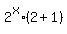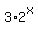    - the left side of the given equation is  2%5E%28x%2B1%29+%2B+2%5Ex = 2%5Ex%2A%282%2B1%29 = 3%2A2%5Ex  and has "3" as a factor in degree 1;


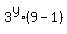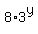    - the right side of the given equation is  3%5Ey%2A%289-1%29 = 8%2A3%5Ey and has  "3" as a factor in degree "y".


Hence,  y = 1,   and the rest is easy.