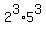If you build a table of the set {1} U {Primes less than 9} you can get unique products.
For each line of the table, consider the sum x+y<9 and filter appropriately by looking at earlier lines to ensure that number combination has not been covered already. The only additional tricky part is
you must consider powers of x and y that are greater than 1:
x y
1 1,2,3,5,7, 4 ( 
)
2 3,4,5
3 3,4,5
5 none
7 none
4 4
覧覧覧覧
That's 13 unique products (1,2,3,5,7,4, 6,8,10, 9,12,15, 16)
覧覧覧覧
Tutor Alan3354's answer is incorrect, even with his assumptions. He's made an assumption about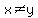 
which is not stated in the problem. Also, x,y not equal to zero is implied by the question ("positive integers" excludes 0. Remember that: zero is neither positive nor is it negative).
覧覧覧覧覧覧覧
Reply to the student: a 'table' is just a list of values (did you ever make a multiplication table?). In my case, I listed x values in one column and corresponding values of y that go with that value of x. So looking at the first row: x is 1, y can take on 1, 2,3,5,7, and 4, giving products xy = 1,2,3,5,7, and 4, respectively.
I listed primes because the Fundamental Theorem of Arithmetic says any number can be written as the product of a unique number of prime numbers (if you don't know this theorem, look it up and learn it).
Thus, a unique product of primes (including repeats, or powers > 1) is a unique number. The 'filtering' I refer to is this: one must be careful not to just reverse the order and think its a new number (e.g. row 2 has x=2, y=3 which will produce 6, so in row for x=3 you don't want to list y=2 because 3*2 =6 which is just the result of a trivial reversal of x and y).
Remember, in building the table, I had the following criteria in mind:
1. x and y must be positive integers (that mean x and y are both integers greater than zero)
2. x+y < 9, this was a restriction in the question you posted.
3. xy is a unique product (so one doesn't treat yx like its different than xy).
Notice in my answer I have provided spaces to help correlate back to the row from which those products came.
覧覧覧覧覧覧
Examples of the Fundamental Theorem of Arithmetic (FTArith):
5 = 5 (5 is a prime number, only 1 and 5 divide evenly into 5) NOTE: 1 is NOT prime.
14 = 2*7 (FTArith says 14 can ONLY be broken down to 2*7, no other product of primes will give you 14)
28 = 
56 =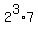 
53352 =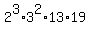 
10 = 2*5
100 = 
1000 = 
