SOLUTION: If (x+ysqrt3)^2 = 48+ 24sqrt3, find the values of x and y, given that they are rational.

Algebra ->  Equations -> SOLUTION: If (x+ysqrt3)^2 = 48+ 24sqrt3, find the values of x and y, given that they are rational.      Log On


   

Question 1111112: If (x+ysqrt3)^2 = 48+ 24sqrt3, find the values of x and y, given that they are rational.
Answer by ikleyn(52790) About Me  (Show Source):
You can put this solution on YOUR website!
.
It is straightforward. 

x^2 + 3y^2 = 48
2xy        = 24    ====>  xy = 24%2F2 = 12.


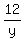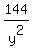
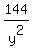x = 12%2Fy   x^2 = 144%2Fy%5E2

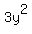144%2Fy%5E2 + + 3y%5E2 = 48

144 + 3y^4 = 48y^2

3y^4 - 48y^2 + 144 = 0

y^4 - 16y^2 + 48 = 0

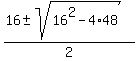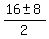y%5E2 = %2816+%2B-+sqrt%2816%5E2+-+4%2A48%29%29%2F2 = %2816+%2B-+8%29%2F2.


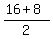1)  y^2 = %2816+%2B+8%29%2F2 = 12  ====>  y is irrational  ===>  the solution does not work;


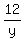2)  y^2 = %2816+-+8%29%2F2 = 4  ====>  y = +/-2  ====>  x = 12%2Fy = +/- 6.


Answer.  Two solutions are  (x,y) = (6,2);  (x,y) = (-6,-2).

Solved.