SOLUTION: Find the volume of the pyramid enclosed in the first octant by the origin and the intercepts of the plane x + 2y + z = 6.

The base of the pyramid is the right-angled triangle in the plane z= 0 with the vertices


(x,y,z) = (0,0,0),  (x,y,z) = (6,0,0),  (x,y,z) = (0,3,0).


The area of this triangle is  A = 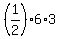 = 9 square units.


The height of the pyramid  is  6 units long  (it is the segment  from the origin (0,0,0)  to the point  (x,y,z) = (0,0,6) ).


Hence, the volume of the pyramid   V =  =  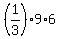= 18 cubic units.