Question 1110991: The locker problem
Imagine a long row of numbered lockers, from 1 to 100 say.
The 1st student starts at #1 and goes down the row opening all the lockers.
The 2nd student starts at #2 and changes every 2nd locker: She'll touch locker #2, 4, 6, 8 etc.
If the locker was open, she closes it,
If the locker was closed, she opens it.
The 3rd student starts at #3 and changes every 3rd locker: She'll touch locker #3, 6, 9, 12 etc.
If the locker was open, she closes it,
If the locker was closed, she opens it.
Etc...
Which lockers end up opened? Why?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! 
Lockers that get touched an odd number of times (1, 3, 5, etc) would end up open.
Lockers that are touched an even number of times, will be opened and closed half of that number of times, and will end up closed.
Lockers are touched as many times as their number of divisors.
If the prime factorization of a number is
it will have divisors of the form  , with
 ,  ,  , etc.
As there are 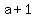 choices for  ,  choices for  , and so on,
the number of divisors is  .
The only way for that product to be odd, is for all exponents in the prime factorization to be even.
That happens if and only if the number is a perfect square.
|
|
|
