SOLUTION: Problem Page Suppose that there are two types of tickets to a show: advance and same-day. The combined cost of one advance ticket and one same-day ticket is $45 . For one performan

Algebra ->  Linear-equations -> SOLUTION: Problem Page Suppose that there are two types of tickets to a show: advance and same-day. The combined cost of one advance ticket and one same-day ticket is $45 . For one performan      Log On


   

Question 1110761: Problem Page Suppose that there are two types of tickets to a show: advance and same-day. The combined cost of one advance ticket and one same-day ticket is $45 . For one performance, 40 advance tickets and 20 same-day tickets were sold. The total amount paid for the tickets was $1300 . What was the price of each kind of ticket?
Answer by ikleyn(52775) About Me  (Show Source):
You can put this solution on YOUR website!
.
Combine the tickets in groups in this way:


 40 advance tickets + 20 same day tickets = 

(20 advance tickets + 20 same say tickets) + 20 advance tickets.


Now the total cost is


1300 = 20*45 + 20a,  where "a" is the cost of the advance ticket.


It gives  20a = 1300-900 = 400.


Hence,  a = 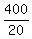400%2F20 = 20 dollars is the price of one advance ticket.


Then the price of one same day ticket is  45-20 = 25 dollars.

Solved.


        The lesson to learn from this solution:   You do not need to solve the system of equations to get the answer.