Question 1110588: Find the exact radian value of the reference angle of the given angle in radians with the works please , i'll appreciate it.
θ =38π/11
θ = 4radians
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! We like to "reference" an acute (or right) angle  , such that , such that  , ,
because we can visualize such an angle in a right triangle.
So, when we find an angle that does not fit in that first quadrant interval,
we find a "symmetrical" reference angle in the first quadrant, because we know that, give or not a minus sign,
the trigonometric function values of both angles will be the same.

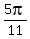 is between is between  and and  , ,
so it is less than a  right angle, right angle,
but  is is  counterclockwise turns, counterclockwise turns,
or  quadrants. quadrants.
The symmetrical reference angle, in the first quadrant is


The coordinates of 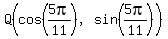 and and 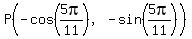 have the same absolute value, have the same absolute value,
but with  being in the third quadrant, being in the third quadrant,
both of the coordinates of  are negative. are negative.
 and and
 , ,
so  is in the third quadrant, with is in the third quadrant, with 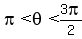 . .
Just as before, for the third quadrant we add or subtract  (a half turn), (a half turn),
as many times as needed,
until we get to the first quadrant.
The reference angle is 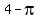
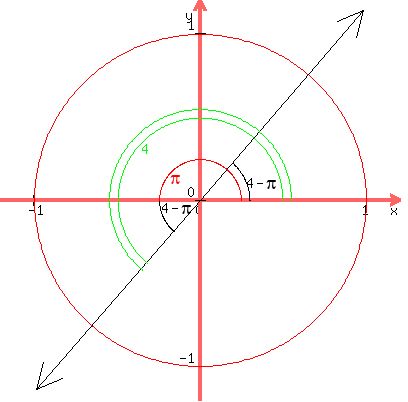
NOTE:
For second quadrant, and fourt angles,
the first quadrant reference angle can be found,
by adding and/or subtracting  as many times as needed as many times as needed
to get to an angle between  and and 
(in the second quadrant, but less than one whole turn),
and then subtracting that angle from  to get the supplementary angle. to get the supplementary angle.
For example,  is is
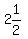 (or (or  counterclockwise turns, or counterclockwise turns, or  half turns) half turns)
plus 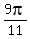 . .
Subtracting those  , we get , we get 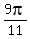 , ,
with  . .
Then,  is the first quadrant reference angle. is the first quadrant reference angle.
|
|
|