|
Question 1109976: Heather drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 12
hours. When Heather drove home, there was no traffic and the trip only took 8
hours. If her average rate was
20 miles per hour faster on the trip home, how far away does Heather live from the mountains?
Do not do any rounding.
Found 3 solutions by ikleyn, stanbon, greenestamps:
Answer by ikleyn(52817)   (Show Source):
You can put this solution on YOUR website! .
Let "r" be the slower rate, in miles per hour.
Then the faster rate is (r+20) mph.
The distance is 12r miles on the way to the mountains.
The distance is 8*(r+20) on the way back.
The distances are the same, so
12r = 8*(r+20) ====> 12r = 8r + 160 ====> 4r = 160 ====> r = 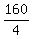 = 40.
Answer. The slower rate is 40 mph, and the one-way distance is 12*40 = 480 miles.
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! Heather drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 12 hours. When Heather drove home, there was no traffic and the trip only took 8 hours. If her average rate was 20 miles per hour faster on the trip home, how far away does Heather live from the mountains?
Do not do any rounding.
-----
Going DATA:
time = 12 hrs ; rate = r mph ; distance = 12r miles
------
Return DATA:
time = 8 hrs ; rate = r+20 ; distance = 8r + 160 miles
--------
Equation:
dist = dist
12r = 8r+160
4r = 160
rate = 40 mph (going rate)
Ans: dist = 12*40 = 480 miles
Cheers,
Stan H.
-----------
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Two good answers from other tutors....
Now here is a non-traditional method that is faster for me.
The ratio of times is 12:8, or 3:2. Since the distances going and coming are the same; the ratio of speeds is 2:3.
So let 2x be the speed on the way there; let 3x be the speed on the way back.
Her speed on the trip home was 20mph faster:
Her speed going was 2x = 40mph; her speed returning was 3x = 60mph. Either calculation 12*40 or 8*60 will give you the distance, which is 480 miles.
|
|
|
| |
