SOLUTION: solve the following equation by row reducing to echlon form 3x+5y=9 2x+3y=5

Algebra ->  Linear-equations -> SOLUTION: solve the following equation by row reducing to echlon form 3x+5y=9 2x+3y=5      Log On


   

Question 1109954: solve the following equation by row reducing to echlon form
3x+5y=9
2x+3y=5
Found 2 solutions by josgarithmetic, greenestamps:
Answer by josgarithmetic(39623) About Me  (Show Source):
You can put this solution on YOUR website!
If Elimination Method is chosen,

system%286x%2B10y=18%2C6x%2B9y=15%29


system%289x%2B15y=27%2C10x%2B15y=25%29
-
(That should still help, even if you want Matrix instead, to reduce.)

Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


There are many different possible paths to take in reducing the matrix to row echelon form....

The original matrix A:
matrix%282%2C3%2C3%2C5%2C9%2C2%2C3%2C5%29

First step: make A(1,1)=1.
You could divide row 1 by 3; but that introduces fractions. It is already easy enough, in the Gauss-Jordan elimination process, to make simple arithmetic errors, without introducing fractions. So my choice for making A(1,1)=1 id to replace row 1 with (row 2 - row 1):
matrix%282%2C3%2C1%2C2%2C4%2C2%2C3%2C5%29

Step 2: make A(2,1)=0.
We have no choice here; we need to use the 1 in A(1,1) to make A(2,1) equal to 0. Replace row 2 with (row 2 - 2*row 1):
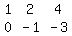
matrix%282%2C3%2C1%2C2%2C4%2C0%2C-1%2C-3%29

Step 3: make A(2,2)=1.
This one is simple -- multiply row 2 by -1:
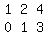
matrix%282%2C3%2C1%2C2%2C4%2C0%2C1%2C3%29

Step 4: make A(1,2)=0.
Again we have no choice but to use the 1 in A(2,2). Replace row 1 with (row 1 - 2*row 2):
matrix%282%2C3%2C1%2C0%2C-2%2C0%2C1%2C3%29

The matrix is now in reduced row echelon form.

The solution to the system is x=-2, y=3.