Question 110971This question is from textbook
: explain why a polynomial function of even degree cannot have an inverse.
This question is from textbook
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! first recall the 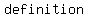 of inverse: of inverse:
A function  with domain with domain  is said to be is said to be 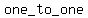 if if 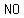
distinct points in  have same have same  under under  , that is: , that is:
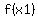 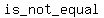 to to 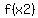 whenever whenever 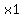 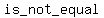 to to 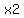 , and ( , and (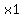 , ,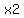 ) is element of ) is element of  . .
Why a polynomial function of even degree cannot have an inverse?
Simply, because a polynomial function of even degree is 
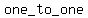 function. function.
Each value of  squared, raised to squared, raised to 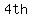 degree, or higher even degree, or higher even
degree, will be that same value; for example,  , and also , and also  . This means that two distinct points in . This means that two distinct points in  have same have same 
under  . .
example:
let 
let domain  be equal to be equal to  , , , , , , , ,
find 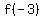 , , 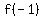 , , , , , ,





as you can see, 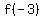 and and  have same image under have same image under 
also 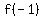 and and  have same image under have same image under 
|
|
|