Question 1109503: Solve and Graph:
2x -y =/< 2
-3x - y =/< 5
-2 =/< x
so far what I have gotten is:
2(-2) - y =/<2
-4-y =/< 2
-y = 2+4
-y = 6
y = -6
SO xy intercepts are (-2, -6)?
and
-3x - y =/<5
-3(-2) - y =/< 5
-6- y=/<5
-y =/< 5 +(-6)
-y = -1
y = 1
So xy intercepts are (-2, 1)?
am I missing any steps?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! You are missing something,
and what you have is not much help to do the graph,
but you also did some unnecessary work.
I suggest to think of the graph of the inequalities first,
and after that do any necessary calculations.
Here is how I would do it (with lots of explanations just for you,
and just a few calculations that your teacher may want to see).
Maybe your teacher will only want to look at the final graph.
If your teacher does not like my way, I am sorry, but I think it is efficient.
If you find a more efficient way,
please let me know in a "thank you" note through this website.
I am not too old to learn a better way.
STEP 1: Sketch/graph the boundary lines.
a) An inequality with a  , like the ones in your question, , like the ones in your question,
includes the boundary line expressed by the equation with the  . .
Because the boundary line is included in the solution to the inequality,
the line is graphed as a solid (not dashed) line.
(If the inequality sign was 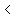 or or 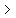 , ,
you would graph the boundary line as a dashed line.
For your problem, the boundary lines are
 , ,  , and , and  . .
Once you do have graphed the lines, you would have

b) There are many ways to graph a line.
A line like  is, obviouly, is, obviouly,
all the points with that  value, value,
a "vertical" line.
If the equation of a line involves  and and  , ,
a little more work is required.
If you have "quad ruled" paper, or graph paper, it will be easier.
You can download and print your own.
To graph a line with that paper,
you just need to plot two points and connect them with a straight line.
Some points may be obvious.
For example, it is obvious that 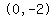 , with , with  , ,
is a point that satisfies 
It is also obvious that 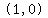 , with , with  , ,
is a point on the graph of  too. too.
Sometimes, you can make  and/or and/or  in the equation of a line, in the equation of a line,
and easily find the corresponding value for the other coordinate of the point.
For  , ,  gives you gives you  <--> <-->  , ,
which means point  is part of that blue line. is part of that blue line.
On the other hand,  , gives you , gives you  ,--> ,-->  , ,
for point  , which is not that easy to plot accurately. , which is not that easy to plot accurately.
In that case you may want to transform the equation,
for example  --> -->  , ,
and then use the slope of the line, or pick a value  to find the corresponding to find the corresponding  } value. } value.
For example,
 --> -->  --> -->  --> -->  , ,
gives you point  . .
STEP 2: Figure out what region of the x-y plane is the solution to the system.
You could look at each inequality,
and figure out the solution to that particular inequality.
Sometimes you could easily "kill two birds with one stone."
Because these are all linear equations/inequalities,
the solution to each is the half of the x-y plane that is to one side of the boundary line.
For  , the solution is obviously the region , the solution is obviously the region
to the right of the  boundary line. boundary line.
For the other two inequalities, you could do some algebra,
or you could pick a point to one side of the lines and see if it is part of the solution.
I like to pick the origin, point  , with , with  , ,
and in this case it works like a charm.
Substituting  and and  into all three inequalities, you get into all three inequalities, you get
for  , ,  , so , so  is a solution, is a solution,
for  , ,  , so , so  is a solution, is a solution,
and for  , ,  makes makes  a solution too. a solution too.
The conclusion is,
you can move from the origin in all directions up to a boundary line,
and you are within the solution to  . .
The graph of that solution, "shaded" in green, is

STEP 3: Find the coordinates of the important points.
In your work, you sort-of figured out the coordinates of
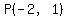 , the intersection/solution of , the intersection/solution of  and and
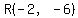 , the intersection/solution of , the intersection/solution of  . .
It turns out that  is not important. is not important.
Besides finding the points we needed to graph the boundary lines,
we are interested in  and and  . .
I used 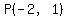 as one of the points to graph as one of the points to graph  . .
I would still like to find  , ,
the intersection/solution of  . .
The solution is 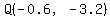 , or if you prefer fractions , or if you prefer fractions 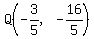 . .
If someone wanted the solution as inequalities rather than as a graph,
I would say  , but I never saw anyone ask for such a thing. , but I never saw anyone ask for such a thing.
You could solve the system by elimination (my choice),
or by substitution:
 --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  --> -->  . .
|
|
|