SOLUTION: What are the restrictions on {{{x}}} for the expression {{{2cosx/cot2x}}}?

Algebra ->  Trigonometry-basics -> SOLUTION: What are the restrictions on {{{x}}} for the expression {{{2cosx/cot2x}}}?      Log On


   

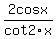Question 1109425: What are the restrictions on x for the expression 2cosx%2Fcot2x?
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
cot%282x%29=cos%282x%29%2Fsin%282x%29 must be defined and must not be zero.
So, the restrictions will arise from
cos%282x%29%3C%3E0 and from sin%282x%29%3C%3E0 .
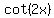When sin%282x%29=0 , cot%282x%29 does not exist/is not defined,
and the function f%28x%29=2cos%28x%29%2Fcot%282x%29 is not defined.
As long as sin%282x%29%3C%3E0 ,
f%28x%29 has the same values as g%28x%29=2cos%28x%29%2Atan%282x%29 ,
but if sin%282x%29=0 f%28x%29+does+not+exist%2C+while+%7B%7B%7Bg%28x%29=0 .
The graphs of f%28x%29 and g%28x%29 look alike,
except that where sin%282x%29=0 the graph of f%28x%29 has a hole.

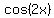When x=pi%2F4 , cos%282x%29=cos%28pi%2F2%29=0 .
When x=3%28pi%2F4%29 , cos%282x%29=cos%283pi%2F2%29=0 .
As cos%282x%29 is a periodic function with period pi ,
the zeros repeat at x=pi%2F4%2Bpi=5pi%2F4 , x=3pi%2F4%2Bpi=7pi%2F4 , and so on.

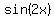When x=0=0%2A%28pi%2F4%29 , sin%282x%29=sin%280%29=0 .
When x=pi%2F2=2pi%2F4 , sin%282x%29=sin%28pi%29=0 .
As sin%282x%29 is a periodic function with period pi ,
the zeros repeat at x=0%2Bpi=pi=4%28pi%2F4%29 , x=pi%2F2%2Bpi=3pi%2F2=6%28pi%2F4%29 , and so on.

At every multiple of pi%2F4 ,
either cos%282x%29=0 or sin%282x%29=0 .

The restrictions can be summarized as highlight%28x%3C%3Ek%28pi%2F4%29%29 for every integer k .

The graph of the function y=2cos%28x%29%2Fcot%282x%29 looks like the one below,
with holes and vertical asymptotes drawn in black: