.
I just saw several (more than one) posts in this forum asking about last four digits of the numbers of the form 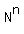 .
.
Probably, it is good time to shed more light on this subject.
Let N be an ARBITRARY fixed natural number (positive integer), and m be another fixed positive integer number.
Consider infinite sequence 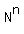 , n = 1, 2, 3, 4, . . .
Then starting from some
, n = 1, 2, 3, 4, . . .
Then starting from some  , the "m" last digits of the numbers
, the "m" last digits of the numbers 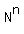 will repeat cyclically.
will repeat cyclically.
This statement seems to be very advanced, but its proof is in couple of lines.
For the sequence 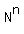 , the sequence of its "m last digits" is the sequence
, the sequence of its "m last digits" is the sequence 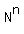 mod
mod 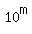 .
There is only finite number of different m-digit numbers, so it will happen INEVITABLY
.
There is only finite number of different m-digit numbers, so it will happen INEVITABLY 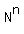 mod
mod 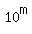 =
=  mod
mod 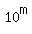 for
some n > k for the first time (the Dirichlet's principle, or so name "pigeons principle").
Then after that this equality will repeat periodically/cyclically.
for
some n > k for the first time (the Dirichlet's principle, or so name "pigeons principle").
Then after that this equality will repeat periodically/cyclically.