Question 1109352: Henry and Harriet are running around an oval that has a perimeter of 400m. Henry takes two and a half minutes to run a full lap while Harriet takes two minutes to run a full lap. If they both start at the same time and run in the same direction, how long will it take Harriet to lap Henry?
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Henry's speed is  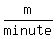 . .
Harriet's speed is  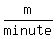 . .
in  minutes Henry will have run minutes Henry will have run 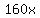 meters, meters,
and Harriet will have run 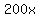 meters. meters.
When Harriet laps Henry,
she will have run 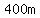 (one full lap) longer than Henry. (one full lap) longer than Henry.
That translates as
 . .
Solving that equation:




 . .
It seems to be that Harriet will lap Henry after  . .
Let's verify.
In 10 minutes Harry will have run  , ,
and Harrriet will have run  . .
NOTE: We did not need to know the size of the track, because we could have measure their speeds in laps per minute instead of meters per minute.
For this particular problems, we could also have figured out the answer by listing how long it took for Henry and for Harriet to run 1, 2, 3, 4, 5, ... laps.
For Henry:
 . .
For Harriet:
 . .
It would not have been so easy, if Harriet had lapped Henry after 4.3 laps for Henry and 5.3 laps for Harriet.
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let L be the "oval perimeter" length.
The condition says that L = 400 meters.
But in reality, with all other given data, the solution below is VALID for any value of L: it DOES NOT DEPEND on the concrete value of L
1. Short Physics solution
Henry' speed is 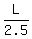 units of L per minute.
Harriet' speed is units of L per minute.
Harriet' speed is 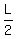 units of L per minute.
The relative speed is units of L per minute.
The relative speed is 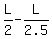 = = 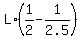 = = 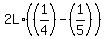 = = 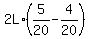 = =  = = 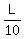 units of L per minute.
It means that after start, the distance between Harriet (who runs faster) and Henry will increase at the rate of units of L per minute.
It means that after start, the distance between Harriet (who runs faster) and Henry will increase at the rate of 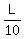 per minute.
Hence, Harriet will win one lap in 10 minutes.
Notice that the solution does not depend on the concrete value of L. per minute.
Hence, Harriet will win one lap in 10 minutes.
Notice that the solution does not depend on the concrete value of L.
2. - Algebra solution
The distance along the oval from the starting point is
D1 = 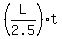 for Henry (=speed*time)
D2 = for Henry (=speed*time)
D2 = 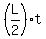 for Harriet.
The condition D2 -D1 = L is for Harriet.
The condition D2 -D1 = L is
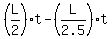 = L, = L,
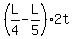 = L, = L,
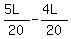 = L, = L,
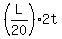 = L, = L,
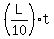 = L
and gives, finally, the same answer t = = L
and gives, finally, the same answer t =  = 10 minutes. = 10 minutes.
Solved.
---------------
To see many other similar (or closely related) solved problems, look into the lesson
- Problems on bodies moving on a circle
in this site.
|
|
|