Question 1109226: The sum of two numbers is 11. The greater is divided by the lesser(smaller) the partial quotient (answer without remainder) is 2. Find the numbers using algebra.
Answer by greenestamps(13216)   (Show Source):
You can put this solution on YOUR website!
You undoubtedly posed the question incorrectly. The way you stated the problem, there are an infinite number of answers.
But if you state the problem correctly, by saying that the two numbers are integers, then there is only one answer.
Let the smaller number be x; then, since the sum of the two numbers is 11, the larger is 11-x.
The problem tells us that when 11-x is divided by x, the whole number part of the answer is 2. So 11-x divided by x must be between 2 and 3:
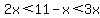 (we don't need to worry about multiplying by x, because we know x is positive)
 and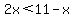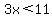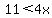 
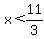 and 
 and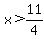 
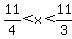
There are of course an infinite number of values of x between 11/4 (2 3/4) and 11/3 (3 2/3). But there is only one integer, 3 between those two numbers.
So the smaller number, x, is 3; the larger number is 11-x = 11-3 = 8.
Checking, we see when 8 is divided by 3 the whole number part of the quotient is 2, as required.
|
|
|
