SOLUTION: If you have 10 dimes and nickels in your pocket that total to $0.70, how many separate dimes and how many separate nickels do you have.

Let d be the number of dimes and n be the number of nickels.

Then you have this system of two equations

  d +   n =  10,        (1)    (counting dimes)
10d +  5n =  70.        (2)    (counting cents)


To solve it, multiply eq(1) by 5. You will have

 5d +  5n =  50,        (1')
10d +  5n =  70.        (2')


Next subtract (1') from (2'). You will get

10d - 5d = 70 - 50,

 5d = 20  ====>  d = 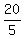 = 4.


There are 4 dimes and 10-4 = 6 nickels.


Check.   4*10 + 6*5 = 70.    !  Correct !


Answer.  There are 4 dimes and 10-4 = 6 nickels.

Let  d be the number of dimes.

Then the number of nickels is (10-d). 

The nickels contribute 5*(10-d) cents toward the total.
The dimes   contribute 10*d     cents toward the total.

The total is  5*(10-d) + 10*d   cents.

From the other side, it is 70 cents, according to the condition.

It gives you an equation

5*(10-d) + 10*d = 70.     


Simplify and solve for n:

50 - 5d + 10d = 70 

5d = 70 - 50  

5d = 20  ====>  d = 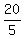 = 4.


There are 4 dimes and 10-4 = 6 nickels.


You got the same answer.

Imagine for a minute that all coins in the parking meter are NICKELS.

Then you would have 10*5 = 50 cents in the parking meter.

But in reality the money amount there is 70 cents, which is 70- 50 = 20 cents more than 50 cents.

Why we have this difference ?  - But of course, because we counted 10-cent dimes as 5-cent coins.

Then it is clear, that the number of dimes is 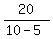  = 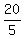 = 4.


And you get the same answer.