SOLUTION: Show that the line y=4x+17 is a tangent to the parabola with equation y=8-2x-x^2

First we need to find common points to the parabola and the straight line.


For it, from the given equations, you have

4x + 17 = 8 - 2x - x^2,     (since left sides of the given equations are identical, their RIGHT sides are equal !)


Then 

x^2 + 6x + 9 = 0.

It is the same as

(x+3)^2 = 0,


and this equation has ONLY ONE real root x= -3.


It means that the straight line and the parabola have ONLY ONE COMMON POINT.


In turn, it means that the given straight line is TANGENT to the parabola..


Thus the STATEMENT in your post is PROVED.






Plots y = 4x+17 (red)  and  y = 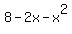 (green)