Question 1108359: Solve :
1/|2x-1| greater than or equal to 1
Found 2 solutions by greenestamps, TeachMath:
Answer by greenestamps(13214)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Solve: 
I'll show a couple of different ways you could solve this. You should know and understand both methods; in any given problem one or the other might be easier to use.
And there are undoubtedly other methods; perhaps you will get answers from other tutors that show you method(s) that are different than these two.
(1) One thing you can do is determine the values of x for which the expression is undefined and the values for which equality holds. That will divide the number line into segments; you can then check in which of those segments of the number line the inequality is satisfied.
The left side of the inequality is undefined when the denominator is 0; that is at x = 1/2.
The equation  is satisfied when is satisfied when  , which is when x = 0 and when x = 1. , which is when x = 0 and when x = 1.
So the number line is divided into the segments
(-infinity, 0], [0,1/2), (1/2,1], and [1, infinity).
Picking values in each of these segments shows the inequality is satisfied on [0,1/2) and (1/2,1].
(2) A more traditional algebraic approach is to separate the solution into two cases, depending on whether 2x-1 is positive or negative. (We already know we don't need to check the case where 2x-1 is 0, because that makes the inequality invalid.)
(a) If 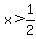 then then  ; then ; then  and the inequality is and the inequality is




So in this case, where we are only considering values of x greater than 1/2, the solution set is all numbers less than or equal to 1; that gives us the (1/2,1] part of the solution.
(b) If 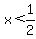 then then 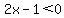 ; then ; then  and the inequality is and the inequality is




So in this case, where we are only considering values of x less than 1/2, the solution set is all numbers greater than or equal to 0; that gives us the [0,1/2) part of the solution.
------------------------------------------------------
I don't know why tutor teachmath bothered to give you an incorrect answer without showing any work.... That's a strange way of interpreting "teach math".
The answer that tutor shows is [0,.5)U[.5,1]. There are two things wrong with that answer:
(1) x=.5 is not included in the solution set, as shown in the second interval of the answer.
(2) the answer is equivalent to [0,1]
Answer by TeachMath(96)   (Show Source): (Show Source):
|
|
|