Question 1108331: What is the equation of a cosine function with an amplitude of 4, a period of 3pi, a horizontal phase shift of pi/4 to the right, and a vertical shift down of 3 units?
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
The general form of a cosine function is
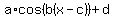
In this form, |a| is the amplitude, c is the (horizontal) phase shift, and d is the vertical shift.
Note that in this form, the coefficient of x must be 1, in order for c to be the correct phase shift.
For b in the formula, you have to do a bit of work: b is 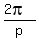 where p is the period.
So in your example, a = 4, b = (2pi)/3pi) = 2/3, c = pi/4, and d = -3.
|
|
|
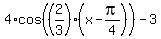
