.
The other tutor's answer is not exactly correct.
In complex domain, 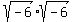 =
= 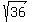 has two (TWO) values: +6 and -6.
Why ? - can you ask me.
Isn't it the product of any two complex numbers is defined by an UNIQUE way ?
Yes, it is true, the product of two complex numbers is defined by an UNIQUE way. There is no doubt.
But in complex domain,
has two (TWO) values: +6 and -6.
Why ? - can you ask me.
Isn't it the product of any two complex numbers is defined by an UNIQUE way ?
Yes, it is true, the product of two complex numbers is defined by an UNIQUE way. There is no doubt.
But in complex domain,  has itself TWO values: 6i and -6i.
They are TWO absolutely symmetric complex instances with equal rights to exist and with equal rights to represent
has itself TWO values: 6i and -6i.
They are TWO absolutely symmetric complex instances with equal rights to exist and with equal rights to represent  .
If you multiply
.
If you multiply 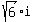 by
by 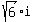 , you will get -6.
If you multiply
, you will get -6.
If you multiply 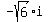 by
by 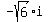 , you will get -6, too.
But if you multiply
, you will get -6, too.
But if you multiply 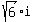 by
by 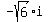 , you will get 6.
Symmetrically, if you multiply
, you will get 6.
Symmetrically, if you multiply 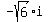 by
by 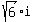 , you will get 6, too.
Therefore, there is NO CONTRADICTION in getting two values, +6 and -6, of the product
, you will get 6, too.
Therefore, there is NO CONTRADICTION in getting two values, +6 and -6, of the product 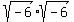 .
If you want to avoid getting of two values when you multiply
.
If you want to avoid getting of two values when you multiply  by
by  , you MUST to point EXACTLY,
which of the two values of
, you MUST to point EXACTLY,
which of the two values of  you mean as one of the two possible instances for each multiplier.
you mean as one of the two possible instances for each multiplier.