Question 1107579: Please help.
How to get the value of cot((3/2)x)? (if x=tan^-1(7/25))
Thank you.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! FOR AN APPROXIMATE VALUE:
You use a calculator or computer to find 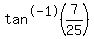
and find that it is approximately
 (in radians) or (in radians) or  . .
Then, you multiply that times  to get to get
 or or  . .
Finally, you find the cotangent of that angle.
If your calculator does not have cotangent,
you can find the approximate value for tangent,
 , ,
and then find the approximate value for cotangent as

FOR AN EXACT VALUE:
Step 1:
Look for a list of trigonometric identities.
(A search brings up Wikipedia, and you find what you need there).
Step 2:
Figure out how to express 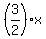 in a way that those trigonometric identities will help you find the answer. in a way that those trigonometric identities will help you find the answer.
Here is how I would do it:
 or or  . .
Looking at the trigonometric identity formulas,
it seems that the easiest way is to first find  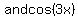 , ,
and then to find 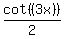 say say 
and use 
At this point, I would check to make sure I had copied the problem right,
because it would be a much kinder problem if it were 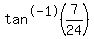 . .
In that case, the angle would be as shown below:
 with with  . .
 is defined as the angle is defined as the angle  , with , with 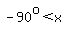 , ,
such that  . .
As the tangent is positive, the angle must be positive.
So,  is a slightly smaller angle than the one in the drawing above, is a slightly smaller angle than the one in the drawing above,
the hypotenuse of the triangle for that case would be
 , ,
and we get ugly expressions for sine and cosine:
 and and  . .
Using the trigonometric identities for triple angles, we get

and

Then, using the half-angle identity for cotangent
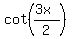  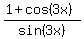  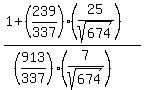  
|
|
|