Question 110757: Write the equation of the line passing through (3, -3) and (3,-6)
Which is the ordered pairs (0,0) (-2, 10), (-1,-5), (-3,9) are solutions for the equation y=5x?
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! #1
| Solved by pluggable solver: Finding the Equation of a Line |
First lets find the slope through the points ( , , ) and ( ) and ( , ,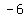 ) )
 Start with the slope formula (note: ( Start with the slope formula (note: ( , ,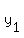 ) is the first point ( ) is the first point ( , , ) and ( ) and ( , ,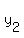 ) is the second point ( ) is the second point ( , ,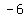 )) ))
 Plug in Plug in  , , , , , , (these are the coordinates of given points) (these are the coordinates of given points)
 Subtract the terms in the numerator Subtract the terms in the numerator 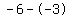 to get to get  . Subtract the terms in the denominator . Subtract the terms in the denominator 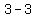 to get to get 
Since the denominator is zero, the slope is undefined (remember you cannot divide by zero). So we cannot use the slope intercept form to write an equation. So we can only say that the equation is a vertical line through  , which means the equation is , which means the equation is  (notice this is not in slope-intercept form) (notice this is not in slope-intercept form)
So the equation  looks like this: looks like this:
 Graph of Graph of  through the points ( through the points ( , , ) and ( ) and ( , ,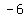 ) )
|
#2
 Start with the given equation Start with the given equation
Let's test the first solution (0,0):
 Plug in Plug in  and and 
 Simplify. Since the two sides of the equation are equal, this means (0,0) is a solution to Simplify. Since the two sides of the equation are equal, this means (0,0) is a solution to 
-------Now lets test another solution-------
Let's test the second solution (-2,10):
 Plug in Plug in  and and 
 Simplify. Since the two sides of the equation are not equal, this means (-2,10) is not a solution to Simplify. Since the two sides of the equation are not equal, this means (-2,10) is not a solution to 
-------Now lets test another solution-------
Let's test the third solution (-1,-5):
 Plug in Plug in  and and 
 Simplify. Since the two sides of the equation are equal, this means (-1,-5) is a solution to Simplify. Since the two sides of the equation are equal, this means (-1,-5) is a solution to 
-------Now lets test another solution-------
Let's test the fourth solution (-3,9):
 Plug in Plug in  and and 
 Simplify. Since the two sides of the equation are not equal, this means (-3,9) is not a solution to Simplify. Since the two sides of the equation are not equal, this means (-3,9) is not a solution to 
==============================================================================
Answer:
So the following ordered pairs are solutions to 
(0,0) and (-1,-5)
Now let's graph the equation  and plot the points (0,0), (-2,10), (-1,-5), and (-3,9) and plot the points (0,0), (-2,10), (-1,-5), and (-3,9)
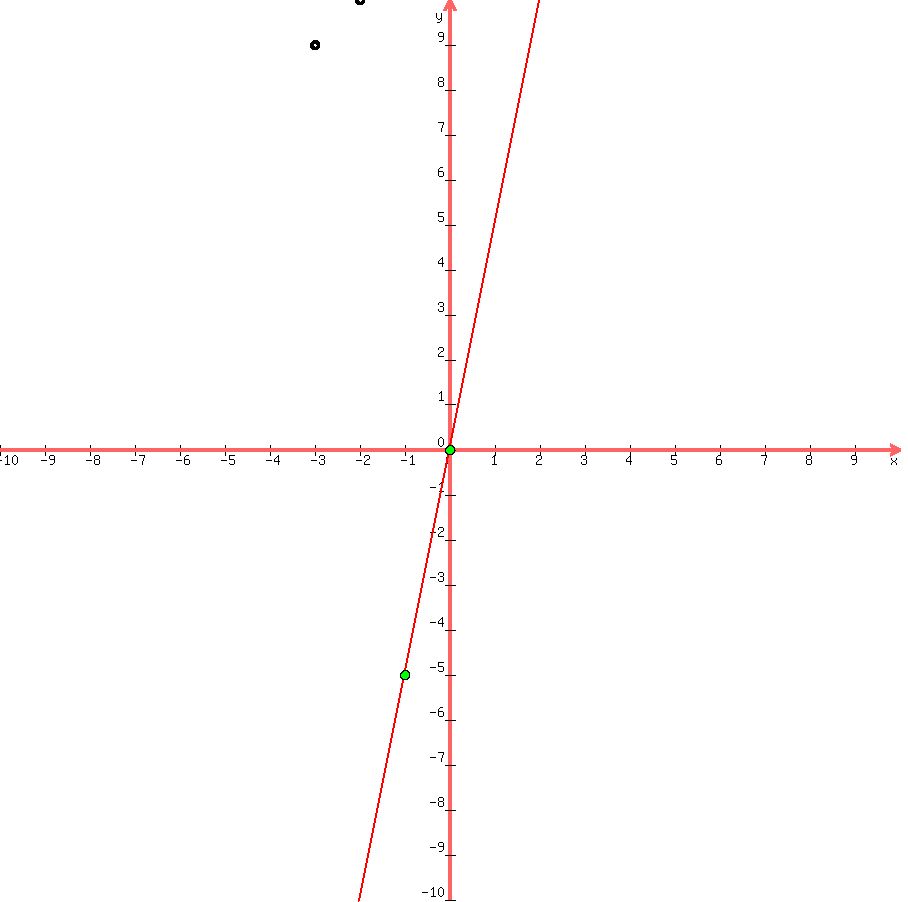
Here we can see that the points (0,0) and (-1,-5) lie on the line (they are the green points). These are the solutions to the equation  . .
Notice the other possible solutions are points that do not lie on the line. Those ordered pairs do not satisfy the equation 
|
|
|