.
If a quadratic polynomial is divided by (x-2) and (x+1) leave the remainder 11 and 1 respectively, find the polynomial.
~~~~~~~~~~~~~~~~~~
The formulation of this problem is not precisely correct.
The correct formulation is THIS:
If a quadratic polynomial with the leading coefficient of 1, when divided by (x-2) and (x+1)
leaves the remainder 11 and 1 respectively, find the polynomial.
Solution
Let P(x) = 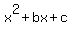 be this quadratic polynomial with unknown coefficients "b" an "c".
The fact that P(x) leaves the remainder 11 when divided by (x-2) is equivalent (according to the "Remainder Theorem") that
P(2) = 11, or
be this quadratic polynomial with unknown coefficients "b" an "c".
The fact that P(x) leaves the remainder 11 when divided by (x-2) is equivalent (according to the "Remainder Theorem") that
P(2) = 11, or  = 11. (1)
The fact that P(x) leaves the remainder 1 when divided by (x+1) is equivalent (according to the same theorem) that
P(-1) = 1, or
= 11. (1)
The fact that P(x) leaves the remainder 1 when divided by (x+1) is equivalent (according to the same theorem) that
P(-1) = 1, or  = 1. (2)
Thus we have this system of two equations to find the coefficients "b" and "c":
2b + c =
= 1. (2)
Thus we have this system of two equations to find the coefficients "b" and "c":
2b + c =  , or 2b + c = 7, (1')
-b + c =
, or 2b + c = 7, (1')
-b + c = 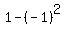 , or -b + c = 0 (2')
To solve the system, subtract eq(2') from eq(1') (both sides). You will get
2b - (-b) = 7 - 0, or 3b = 7 ====> b =
, or -b + c = 0 (2')
To solve the system, subtract eq(2') from eq(1') (both sides). You will get
2b - (-b) = 7 - 0, or 3b = 7 ====> b =  .
Then from eq(2') c = b =
.
Then from eq(2') c = b =  .
Thus the quadratic polynomial is P(x) =
.
Thus the quadratic polynomial is P(x) = 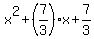 .
Check. P(2) =
.
Check. P(2) = 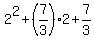 =
= 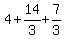 =
= 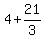 = 4 + 7 = 11, and
P(-1) =
= 4 + 7 = 11, and
P(-1) = 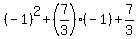 =
=  = 1. ! Correct !
Answer. The polynomial is P(x) =
= 1. ! Correct !
Answer. The polynomial is P(x) = 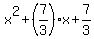 .
.
---------------
On Remainder theorem see the lesson
- Divisibility of polynomial f(x) by a binomial (x-a) and the Remainder theorem
in this site.
To see other similar solved problems, look into the lesson
- Solved problems on the Remainder thoerem
Also, you have this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic
"Divisibility of polynomial f(x) by binomial (x-a). The Remainder theorem".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.