SOLUTION: The sides of a triangle lie along the straight line with equations y=1; x+y=6 and y-3x+2=0. (a) Find the equation of the altitudes. (An altitude is a line through a vertex perpend

Algebra ->  Triangles -> SOLUTION: The sides of a triangle lie along the straight line with equations y=1; x+y=6 and y-3x+2=0. (a) Find the equation of the altitudes. (An altitude is a line through a vertex perpend      Log On


   

Question 1107299: The sides of a triangle lie along the straight line with equations y=1; x+y=6 and y-3x+2=0.
(a) Find the equation of the altitudes. (An altitude is a line through a vertex perpendicular to the opposite)
(b) Show that the altitudes are con-current and find the coordinates of the point where they meet (the point is called the orthocentre of the triangle).
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!

a) The vertices are
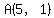A%285%2C1%29 , given by
system%28y=1%2Cx%2By=6%29 --> system%28y=1%2Cx%2B1=6%29 --> system%28y=1%2Cx=5%29 ,
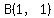B%281%2C1%29 , given by
system%28y=1%2Cy-3x%2B2=0%29 --> system%28y=1%2C1-3x%2B2=0%29 --> system%28y=1%2C3-3x=0%29 --> system%28y=1%2Cx=1%29 , and
C%282%2C4%29 , given by
system%28x%2By=6%2Cy-3x%2B2=0%29 --> system%28x%2By=6%2C3x-y=2%29 --> system%28x%2By=6%2C4x=8%29 --> system%28x%2By=6%2Cx=2%29 --> system%282%2By=6%2Cx=2%29 --> system%28y=4%2Cx=2%29 .
Side AB is the horizontal line y=1 .
The altitude from C%282%2C4%29 to AB , perpendicular to AB
is the vertical line highlight%28x=2%29
Side AC is the line x%2By=6 <--> y=6-x , with slope -1 .
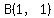The altitude from B%281%2C1%29 to AC , perpendicular to AC
having slope 1, is
y-1=1%28x-1%29 --> y=x-1%2B1 --> highlight%28y=x%29 .
Side BC is the line y-3x%2B2=0 <--> y=3x-2 , with slope 3 .
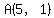The altitude from A%285%2C1%29 to BC , perpendicular to BC
having slope -1%2F3, is
y-1=%28-1%2F3%29%28x-5%29 --> y-1=%28-1%2F3%29x%2B5%2F3 --> y=%28-1%2F3%29x%2B5%2F3%2B1 --> highlight%28y=%28-1%2F3%29x%2B8%2F3%29 .

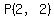
The intersection of x=2 and y=x is given by P%282%2C2%29
system%28x=2%2Cy=x%29 --> system%28x=2%2Cy=2%29 .
The intersection of x=2 and y=%28-1%2F3%29%2B8%2F3 is the solution to
system%28x=2%2Cy=%28-1%2F3%29x%2B8%2F3%29 --> system%28x=2%2Cy=-2%2F3%2B8%2F3%29 --> system%28x=2%2Cy=6%2F3%29 --> system%28x=2%2Cy=2%29 ,
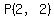also point P%282%2C2%29 .
The intersection of y=x and y=%28-1%2F3%29%2B8%2F3 is the solution to
system%28y=x%2Cy=%28-1%2F3%29x%2B8%2F3%29 --> system%28y=x%2Cx=%28-1%2F3%29x%2B8%2F3%29 --> system%28y=x%2Cx%2B%281%2F3%29x=8%2F3%29 --> system%28y=x%2C%284%2F3%29x=8%2F3%29 --> system%28y=x%2Cx=2%29 --> system%28y=2%2Cx=2%29 ,
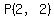also point P%282%2C2%29 .