SOLUTION: the equation of a line 3x-2y=20 what point on the line is equidistant from the points A(1,-1) and B(1,8)

Algebra ->  Circles -> SOLUTION: the equation of a line 3x-2y=20 what point on the line is equidistant from the points A(1,-1) and B(1,8)      Log On


   

Question 1106795: the equation of a line 3x-2y=20 what point on the line is equidistant from the points A(1,-1) and B(1,8)
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630) About Me  (Show Source):
You can put this solution on YOUR website!
Here is a start.
The line is y=3x%2F2-10 which is a general point ( x, 3x%2F2-10 ).

Using Distance Formula and squaring both sides, Line to A equals Line to B;
%28x-1%29%5E2%2B%283x%2F2-10-1%29%5E2=%28x-1%29%5E2%2B%283x%2F2-10-8%29%5E2
Simplify and solve for x;
.
.
-33x%2B121=-54x%2B324
.
.

Answer by ikleyn(52887) About Me  (Show Source):
You can put this solution on YOUR website!
.
the equation of a line 3x-2y=20 what point on the line is equidistant from the points A(1,-1) and B(1,8)
~~~~~~~~~~~~~~~~~ 

The point under the question is the intersection point of the given line with the perpendicular bisector to the line segment
connecting the given points A(1,-1)  and  B(1,8). 


Notice that the line connecting these points is VERTICAL line x = 1.


Hence, the perpendicular bisector is the horizontal line  y = 3.5   (where 3.5 = 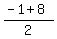%28-1%2B8%29%2F2 ).


The intersection point is that you will obtain after substituting y = 3.5 into the equation of the given line:

3x - 2y = 20  at  y = 3.5  becomes  3x - 2*3.5 = 20  ====>  3x = 20+7 = 27  ====>  x = 27%2F3 = 3.


Hence, the point you are seeking for is (2,3.5).


Thus you can solve this problem  MENTALLY,  without solving ANY equations.