Question 1106487: Evaluate √(7/3+√(7/9+√(7/3+√(7/9+⋯)) ) )
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x = sqrt(7/3+sqrt(7/9+sqrt(7/3+sqrt(7/9+...))))
x^2 = 7/3 + sqrt(7/9+sqrt(7/3+sqrt(7/9)...)))
x^2-7/3 = sqrt(7/9+sqrt(7/3+sqrt(7/9)...)))
(x^2-7/3)^2 = 7/9+sqrt(7/3+sqrt(7/9)...))
(x^2-7/3)^2 = 7/9 + x
x^4-(14/3)x^2+49/9 = 7/9 + x
x^4-(14/3)x^2-x+42/9 = 0
x^4-(14/3)x^2-x+14/3 = 0
3x^4-14x^2-3x+14 = 0
This polynomial has two real roots, x=1 and x=2, and a pair of complex roots.
Clearly the given expression is real, because it is the square root of a positive number. And clearly the expression is not equal to 1. Therefore the value of the expression is 2.
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Evaluate 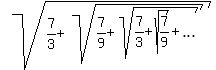
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I just solved similar, but much more simple problem under the link
https://www.algebra.com/algebra/homework/Angles/Angles.faq.question.1106262.html
https://www.algebra.com/algebra/homework/Angles/Angles.faq.question.1106262.html
So, I will assume that it was YOU who requested the preceding problem (because "Lightning never strikes the same place twice").
In other words, I will assume that you are familiar with the idea and the solution of that previous problem.
Based on it, I will be short with this one.
Let us consider, for brewity of writing, more general expression
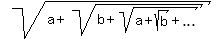 = x,
where a = = x,
where a =  , b = , b =  . Then . Then
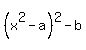 = x. (It is clear, and I will not spend words to justify it . . . )
It is equivalent to = x. (It is clear, and I will not spend words to justify it . . . )
It is equivalent to
 - -  = x, or = x, or
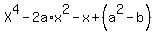 = 0.
Now substitute here a = = 0.
Now substitute here a =  , b = , b =  . You will get this equation in the form . You will get this equation in the form
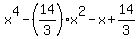 = 0, or, multiplying all the terms by 3 = 0, or, multiplying all the terms by 3
 = 0.
Now I will not go into details, and simply show the plot of the last polynomial.
It clearly shows that x= 2 is the root. And now you can check it MANUALLY (as I did . . . ) = 0.
Now I will not go into details, and simply show the plot of the last polynomial.
It clearly shows that x= 2 is the root. And now you can check it MANUALLY (as I did . . . )
 Plot y =
Plot y = 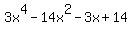 It makes me CONVINCED that
It makes me CONVINCED that 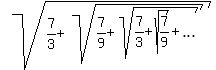 = 2.
Check. = 2.
Check. 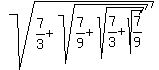 = 1.984 (approx.) = 1.984 (approx.)
Solved.
|
|
|