2x+y+2z=4
2x+2y =5
2x- y+6z=2
Write it this way, putting in 1 coefficients and 0z
fo the missing z-term in the second equation.
2x + 1y + 2z = 4
2x + 2y + 0z = 5
2x - 1y + 6z = 2
Then do it step by step just like this one:
-----------------------------
x+y+z = 6
2x-y+z = 3
x+2y-3z = -4
Write it this way:
1x + 1y + 1z = 6
2x - 1y + 1z = 3
1x + 2y - 3z = -4
Cramer's rule:
There are 4 columns,
1. The column of x-coefficients 
2. The column of y-coefficients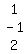 
3. The column of z-coefficients 
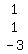4. The column of constants: 
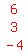There are four determinants:
1. The determinant 
consists of just the three columns
of x, y, and z coefficients. in that order, but does not
contain the column of constants.
.
It has value 
. I'm assuming you know how to find the
value of a 3x3 determinant, for that's a subject all by itself.
If you don't know how, ask me how in the note form below and I'll
get back to you by email. No charge.
2. The determinant 
is like the determinant
except that the column of x-coefficients is replaced by the
column of constants. does not contain the column
of x-coefficients.
.
It has value 
.
3. The determinant 
is like the determinant
except that the column of y-coefficients is replaced by the
column of constants. does not contain the column
of y-coefficients.
.
It has value 
.
4. The determinant 
is like the determinant
except that the column of z-coefficients is replaced by the
column of constants. does not contain the column
of z-coefficients.
.
It has value 
.
Now the formulas for x, y and z are
Edwin
