Question 1106201: A cassette shop charges Rupees 15 for renting a video cassette for the first day. It charges rupees 2 extra for every additional day. What will be the algebraic expression for the amount that Sara would pay. If she rents a video cassette for n days
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39630)   (Show Source): (Show Source):
Answer by ikleyn(52893)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I read and understand the condition differently:
In the first day the shop charges 15 rupees, in the 2-nd day it charges 15+2 = 17 rupees,
in the third day it charges 17+2 = 19 rupees . . . and so on.
What is a bill after "n" days ?
So, it is about finding the sum of the arithmetic progression
15, 17, 19, . . . 15+2(n-1).
The first term is 15, the common difference is 2, and the number of terms = number of days = n.
The answer is: the balance, i.e. the sum of n terms, is  = =  = = 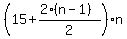 = = 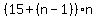 = (14+n)*n. = (14+n)*n.
Solved.
----------------
On arithmetic progressions, see the lessons in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|