SOLUTION: solutions of sin5x + sin3x=0 in the interval [0, 2\pi ]

Use the formula  sin(a) + sin(b) = 2*sin((a+b)/2)*cos((a-b)/2),

which is one of basic formula of Trigonometry.



In your case  a = 5x,  b = 3x.   Hence,

sin(5x) + sin(3x) = 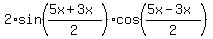 = 2*sin(4x)*cos(x).



Therefore, the original equation is equivalent to

2(sin(4x)*cos(x) = 0.



The last equation deploys in two equations:


    1)  sin(4x) = 0,  which in the given interval has the solutions

        x= 0,  ,    and  ,

and

    2)  cos(x) = 0,  which in the given interval has the solutions

        x=   and  .



Answer.  The four solutions to the original equation are x= 0,  ,    and  .