Question 1105717: If  , where a, b, and c are positive integers, and b < c, evaluate the value of abc. , where a, b, and c are positive integers, and b < c, evaluate the value of abc.
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If  , where a, b, and c are positive integers, and b < c, evaluate the value of abc. , where a, b, and c are positive integers, and b < c, evaluate the value of abc.
~~~~~~~~~~~~~~~~~~~~
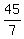 = 6 + = 6 + 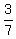 = a + = a + 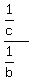 = a + = a +  .
Since "b" and "c" are positive integers with b < c, you can conclude that .
Since "b" and "c" are positive integers with b < c, you can conclude that  < 1.
Hence, a = 6.
But for "b" and "c" you have INFINITELY MANY answers (b,c) = (3,7), (6,14), (9,21) . . . and so on . . .
Therefore, IT IS NOT POSSIBLE to evaluate the value of abc by an UNIQUE way.
Your problem is posed INCORRECTLY. < 1.
Hence, a = 6.
But for "b" and "c" you have INFINITELY MANY answers (b,c) = (3,7), (6,14), (9,21) . . . and so on . . .
Therefore, IT IS NOT POSSIBLE to evaluate the value of abc by an UNIQUE way.
Your problem is posed INCORRECTLY.
|
|
|