SOLUTION: How do you find the radius of a circle inscribed in a scalene triangle

Algebra ->  Customizable Word Problem Solvers  -> Geometry -> SOLUTION: How do you find the radius of a circle inscribed in a scalene triangle       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1105670: How do you find the radius of a circle inscribed in a scalene triangle
Found 3 solutions by KMST, ikleyn, rothauserc:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
Here is a scalene triangle (ABC) with an inscribed circle centered at O.
.
Here is the same sketch with the line segments connecting the circle center
with the vertices of the triangle,
and with the points of tangency with the triangle sides.
.
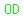green%28OD%29 , green%28OE%29 , and green%28OF%29 ,
connect circle center O to the points of tangency.
They are radii of the circle, R=OD=OE=OF
and they are perpendicular to the sides of the triangle.
So, they are the heights of triangles ABO, BCO, and ACO.

If you know AB=c , BC=a , and AC=b ,
the lengths of the sides of the triangle,
you can calculate the area of triangle ABC
as the sum of the areas of triangles ABO, BCO, and ACO:
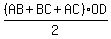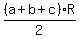%28AB%2BBC%2BAC%29OD%2F2 or %28a%2Bb%2Bc%29R%2F2 .
You could also calculate the area of the triangle using Heron's formula as
sqrt%28s%28s-a%29%28s-b%29%28s-c%29%29 , where s=%28a%2Bb%2Bc%29%2F2 is the semi-perimeter.

If you do not know the semi-perimeter (or the perimeter, or the lengths of all 3 sides of the triangle),
as long as you have enough information to determine what triangle is congruent to that one,
there is a way to find those lengths,
and you could use a similar strategy after you find the needed length(s).

The same strategy would work for any triangle, scalene or otherwise.

If you do not have enough information to find the needed lengths,
you may know that the triangle is scalene,
but you do not know the triangle, and cannot find the radius.
For example, knowing only that the side lengths are in the ratio 3:4:5, or that all 3 angles have different measures would let you know the triangle is scalene, but there would be no way to calculate the radius of the inscribed circle.

Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.
The radius of a  circle inscribed in a scalene triangle is equal to the area of the triangle divided by semi-perimeter:


r = A%2Fs,     (1)


where A is the area and "s" is the semi-perimeter.


Or, equivalently, A = r*s.


For the proof, see the lesson
    - Proof of the formula for the area of a triangle via the radius of the inscribed circle 
in this site.


So, if you know the side lengths of your scalene triangle, you can calculate its area using the Heron's formula, and then use the formula (1).


On Heron's formula, see the lessons
    - Proof of the Heron's formula for the area of a triangle 
    - One more proof of the Heron's formula for the area of a triangle 
in this site.


Answer by rothauserc(4718) About Me  (Show Source):
You can put this solution on YOUR website!
If the sides have length a, b, c, we define the semi-perimeter s to be half their sum, so s = (a+b+c)/2. Given this, the radius is
:
r^2 = (s - a)*(s - b)*(s - c) / s
:
Take the square root of this expression to find r
:
Here we are using Heron's formula to derive the formula for r^2, namely
:
A = s * r
: