SOLUTION: A= {{{a 1 1 1 1}}} {{{1 a 1 1 1}}} {{{1 1 a 1 1}}} {{{1 1 1 a 1}}} {{{1 1 1 1 a}}} (1)calculate det A ? (2)for which value of a

Algebra ->  Finance -> SOLUTION: A= {{{a 1 1 1 1}}} {{{1 a 1 1 1}}} {{{1 1 a 1 1}}} {{{1 1 1 a 1}}} {{{1 1 1 1 a}}} (1)calculate det A ? (2)for which value of a      Log On


   

Question 1105210: A= 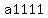a+1+1+1+1
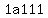
1+a+1+1+1
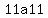
1+1+a+1+1
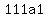
1+1+1+a+1
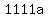
1+1+1+1+a

(1)calculate det A ?
(2)for which value of a will Ax=0 have nonzero solutions?
(3)when ax =a has nonzero solution how many arbitrary constants are there in the general solution?
Found 3 solutions by Alan3354, Edwin McCravy, ikleyn:
Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
A= a+1+1+1+1
1+a+1+1+1
1+1+a+1+1
1+1+1+a+1
1+1+1+1+a

(1)calculate det A ?
-----------
I used an online calculator and found that when I subbed values from 0 to 9 for a, the Det = 968. The calculator would not accept literal values.
=======================
(2)for which value of a will Ax=0 have nonzero solutions?
(3)when ax =a has nonzero solution how many arbitrary constants are there in the general solution?

Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
(1)calculate det A 
matrix%281%2C2%2Cdet%2CA%29%22%22=%22%22

a%28a%5E3-3a%2B2%29-1%28a%5E2-2a%2B1%29%2B1%28-a%5E2%2B2a-1%29-1%28a%5E2-2a%2B1%29%22%22=%22%22
a%5E4-3a%5E2%2B2a-a%5E2%2B2a-1-a%5E2%2B2a-1-a%5E2%2B2a-1%22%22=%22%22

a%5E4-6a%5E2%2B8a-3

Let's see if we can factor that using synthetic division:

1 | 1  0 -6  8 -3
  |    1  1 -5  3 
    1  1 -5  3  0

so a%5E4-6a%5E2%2B8a-3=%28a-1%29%28a%5E3%2Ba%5E2-5a%2B3%29


1 | 1  1 -5  3
  |    1  2 -3
    1  2 -3  0

so now 

and

matrix%281%2C2%2Cdet%2CA%29%22%22=%22%22%28a-1%29%5E3%28a%2B3%29

(2)for which value of a will AX=0 have nonzero solutions? 
When the determinant is not 0.  And since

matrix%281%2C2%2Cdet%2CA%29%22%22=%22%22%28a-1%29%5E3%28a%2B3%29

That will be when

(3)when ax =a has nonzero solution how many arbitrary constants
are there in the general solution?
We row-reduce this augmented matrix:



And we get:



So the only solution is

%22%22=%22%22

That's a unique solution. There are no arbitrary constants, unless 
you want to say that "a" itself 
is the only arbitrary constant and there is 1 arbitrary constant.

Edwin

Answer by ikleyn(52858) About Me  (Show Source):
You can put this solution on YOUR website!
.
A = 

I will calculate the determinant det (A) in two steps.


Step 1


Subtract row 1 from the rows 2, 3, 4 and 5. You will get modified 5x5-matrix B

B = 

Under these transformations (and after these transformations), det (A) = det (B).


Step 2


In matrix B, add all the columns 2, 3, 4 and 5 to the column 1. You will get modified 5x5-matrix C

C = 

Under these transformations (and after these transformations), det (A) = det (B) = det (C).

Now calculate the determinant det (C) using cofactoring along the 1-st column.

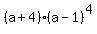You will get  det (C) = %28a%2B4%29%2A%28a-1%29%5E4.


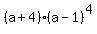Thus  det (A) = %28a%2B4%29%2A%28a-1%29%5E4.


In this way, you can calculate the determinant of the given form matrix for ANY order "n".


So, the question #1 is answered.



The answer to the question #2 is:  


    Ax = 0 has nonzero solutions for a = -4  and for a = 1.



The question #3 is formulated INCORRECTLY, in my view.

The correct formulation is THIS:


    when Ax = 0 has nonzero solution, how many arbitrary constants are there in the general solution?


And the answer to this question is:

    when a = 1,  the general solution has  4  arbitrary constants;

    when a = -4, the general solution has  1 arbitrary constant.