Question 1105148: If 2 ratios are formed at random from the 4 numbers 1,2,4,8, what is the probability that the ratios are equal?
Found 3 solutions by richwmiller, stanbon, ikleyn:
Answer by richwmiller(17219)   (Show Source):
You can put this solution on YOUR website! 1,2,4,8
4*3*2*1/2
24/2 possibilities
How many are true?
1:2 as 4:8
1:4 as 2:8
2:1 as 8:4
4:1 as 8:2
8:4 as 2:1
8:2 as 4:1
4:8 as 1:2
2:8 as 1:4
How many ?
True divided by possibilities =
Answer by stanbon(75887)  (Show Source):
You can put this solution on YOUR website! If 2 ratios are formed at random from the 4 numbers 1,2,4,8, what is the probability that the ratios are equal?
1/2 = 2/4 = 4/8
2/1 = 8/4 = 4/2
1/4 = 2/8
4/1 = 8/2
# of equal pairs is 8
----
# of random pairs = 4P2 = 12
----
P(pairs are equal) = 8/12 = 2/3
---------------
Cheers,
Stan H.
-----------
Answer by ikleyn(52921)  (Show Source):
You can put this solution on YOUR website! .
The table below shows the (4x4)-matrix of all possible ratios
Numerators 1 2 4 8 <<<---=== Denominators
1 1 1/2 1/4 1/8
2 2 1 1/2 1/4
4 4 2 1 1/2
8 8 4 2 1
So, the basic space is the space of 4*4 = 16 ratios in the cells of this matrix.
We randomly select two ratios from this table: so, there are 16*16 = 256 elements in the space of events.
We compare the ratios and count in how many cases they have identical values.
They are identical in 4*4 + (3*3 + 3*3) + (2*2 + 2*2) + 2 = 44 cases:
4*4 for 4 pairs of ratios along the major diagonal;
then (3*3 + 3*3) pairs of ratios along two next "diagonals";
then (2*2 + 2*2) pairs of ratios along two next-next "diagonals";
and, finally, 1+1 = 2 pairs of ratios along the next-next-next "diagonals".
In all, among 256 possible (potential) pairs of ratios, there are 44 cases when they have identical values.
So, the answer to the problem's question is  =  .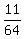
|
|
|
