Question 1104676: A basket contains 11 eggs, 3 of which are cracked. If we randomly select 5 of the eggs for hard boiling, what is the probability of the following events?
a. All of the cracked eggs are selected.
b. None of the cracked eggs are selected.
c. Two of the cracked eggs are selected.
Found 2 solutions by rothauserc, greenestamps:
Answer by rothauserc(4718)   (Show Source):
You can put this solution on YOUR website! a) Probability all 3 of the cracked eggs are selected = (3/11) * (2/10) * (1/9) * (8/8) * (7/7) = 0.006
:
b) P (all 5 are not cracked) = (8/11) * (7/10) * (6/9) * (5/8) * (4/7) = 0.1212
:
c) P (2 cracked eggs are selected) = (3/11) * (2/10) * (8/9) * (7/8) * 6/7) = 0.0364
:
Answer by greenestamps(13215)  (Show Source):
You can put this solution on YOUR website!
Only one of the answers from the other tutor is correct; he left out an important part of his calculations.
a. For the case where all the cracked eggs are selected, he showed the calculation
Taken literally, that calculation shows the probability that the first three eggs selected are the three cracked ones, and the last two are not cracked.
But the cracked and uncracked eggs could be selected in a different order. The number of different orders in which the three cracked eggs and two uncracked eggs could be selected is  .
So the complete calculation for this case is
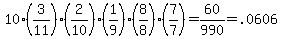
b. For this case, where all the eggs selected are not cracked, the other tutor's answer is correct, because with all the eggs being uncracked, there is no question about the order in which they are selected.
c. For this case his answer is again missing one important factor, due to the fact that we can select 2 cracked eggs and 3 uncracked eggs in many different orders. 10 different orders, in fact -- because the calculation of the number of different orders is exactly the same as for case a.
So where he shows the calculation
 ,
the correct calculation should be
I know when I was first learning the kinds of calculations used in probability, I too found it easy to forget the fact that in cases like these the desired outcome could be achieved in different ways. So I personally found I was less likely to perform the wrong (incomplete) calculation if I used a completely different method for solving this type of probability problem.
In each of the probabilities we are calculating in this problem, we are choosing 5 of the 11 eggs. The number of different ways of choosing 5 of 11 items is 11C5, "11 choose 5". The value of 11C5 is  .
So the denominator of our probability fraction is going to be 462 for all three cases. Let's use the "n choose r" concept to find the numerator for each case and thus to find the probability for each case. Our answers will of course be the same as those we already found.
a. For this case, we need to choose all 3 of the cracked eggs and 2 of the other 8 eggs. The number of ways of doing that is
The probability for this case is then  which is the answer we got by the other method.
b. For this case, we need to choose none of the 3 cracked eggs and 5 of the other 8. The probability of doing that is
c. For this case, we need to choose 2 of the 3 cracked eggs and 3 of the other 8. The probability of doing that is
|
|
|
