Question 1104478: Hi!
7. ABC has vertices A(0, 6), B(4, 6), and C(1, 3). Sketch a graph of ABC and use it to find the orthocenter of ABC. Then list the steps you took to find the orthocenter, including any necessary points or slopes you had to derive.
Could someone really help me on this?
The graph is not needed since I can sketch it myself. I just need help with the steps that need to be taken in order to find the orthocenter.
Thank You So Much!
Found 2 solutions by stanbon, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! ABC has vertices A(0, 6), B(4, 6), and C(1, 3). Sketch a graph of ABC and use it to find the orthocenter of ABC. Then list the steps you took to find the orthocenter, including any necessary points or slopes you had to derive.
Could someone really help me on this?
The graph is not needed since I can sketch it myself. I just need help with the steps that need to be taken in order to find the orthocenter.
Thank You So Much!
------
You need to find the three altitudes of the triangle.
Example::
Using base A(0,6) B(4,6)
slope = (6-6)/(4-0) = 0
So, the base is horizontal
Therefore the altitude is vertical and passes thru C(1,3)
The equation of the altitude must be x = 1
----
Using base A(0,6) C(1,3)
slope = (6-3)/(0-1) = -3
So the altitude must have slope = +1/3 and it must pass thru B(4,6)
Find the equation of that altitude::
Form y = mx + b
Solve for "b":: 6 = (1/3)4 + b
b = 14/3
The equation of that altitude must be y = (1/3)x + 14/3
------
Find the equation of the 3rd altitude.
Then find the intersection of the three altitudes.
That point is the orthocenter.
-----
Cheers,
Stan H.
-----------
Answer by ikleyn(52759)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
ABC has vertices A(0, 6), B(4, 6), and C(1, 3). Sketch a graph of ABC and use it to find the orthocenter of ABC.
Then list the steps you took to find the orthocenter, including any necessary points or slopes you had to derive.
~~~~~~~~~~~~~~~~~~~~~~~~~~
The orthocenter is the point where the three altitudes of a triangle intersect.
Notice that the side AB is horizontal: it lies on the straight line y = 6.
Therefore, the altitude drawn to AB is VERTICAL line, and since it is going through the point C(1,3), its equation is
x = 1. (1)
Next, the side AC has the slope m =  = = 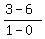 = = 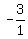 = -3.
Hence, the perpendicular to AC has the slope = -3.
Hence, the perpendicular to AC has the slope  .
Thus, the altitude to the side AC, passing through the vertex B = (4,6), has the equation
y-6 = .
Thus, the altitude to the side AC, passing through the vertex B = (4,6), has the equation
y-6 = 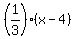 (2)
Equations (1) and (2) have a solution (x,y) = (1,5).
It is the orthocenter. (2)
Equations (1) and (2) have a solution (x,y) = (1,5).
It is the orthocenter.
Answer. The orthocenter is the point (x,y) = (1,5).
--------------
P.S. You do not need the equation of the third altitude.
It is quite enough to have the equations of two altitudes and to find their common solution, which represents the common intersection point.
The third altitude will pass through this point, since the altitudes are concurrent in any triangle.
|
|
|