Question 1104273: If WXYZ is a parallelogram, which of the following must ALWAYS be true?
A. segment WY and segment YX bisect each other
B. angle XWZ is congruent to angle XYZ
C. segment WY is perpendicular to segment ZX
D. segment WY is congruent to segment ZX
E. segment ZX bisects angle WXY
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Parallelograms (and other polygons) are named
by listing letter names of the vertices
in the order you see them as you go around the parallelogram.
So, parallelogram WXYZ would look something like this:
 Line segments WY and XZ are diagonals.
A.  is never true.
Diagonals bisect each other in all parallelograms,
and WY is a diagonal, that bisects diagonal XZ,
but XY is a side that meets diagonal WY and point Y,
which is an endpoint of both segments.
It is not the midpoint of either segment.
B.  must always be true.
Angles XWZ and XYZ are opposite angles in WXYZ,
and opposite angles in a parallelogram are always congruent.
C.  is not always true.
It is true for a rhombus
(or a square that is a special type of rhombus),
but it is not true for other parallelograms,
like the one on the figure above.
D.  is not always true.
It is for a rectangle
(or a square that is a special type of rectangle),
but it is not true for other parallelograms,
like the one on the figure above.
You can see that XZ is much shorter than WY.
E.  is not always true.
It is true for a rhombus
(or a square that is a special type of rhombus),
but it is not true for other parallelograms,
like the one on the figure above.
You can see that angle ZXY, measuring about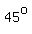 
is much smaller than angle WXZ,
so those two angles adding up to angle WXY are not congruent.
|
|
|
