Question 1104241: If a, b, and c are positive integers, find the sum a+b+c if  , ,  , and , and  = =
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If a, b, and c are positive integers, find the sum a+b+c if  , ,  , and , and 
~~~~~~~~~~~~~~~~~~~~~~~
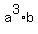 = 1375, (1) = 1375, (1)
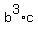 = 3993, (2) = 3993, (2)
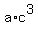 = 135 (3)
implies (after multipluing all three equations, both left and right sides) = 135 (3)
implies (after multipluing all three equations, both left and right sides)
 = 741200625 ====> = 741200625 ====>
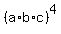 = 741200625 ====> abc = = 741200625 ====> abc = 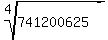 = 165.
Again: abc = 165 = 3*5*11. (4)
3, 5 and 11 are prime integers.
Since = 165.
Again: abc = 165 = 3*5*11. (4)
3, 5 and 11 are prime integers.
Since 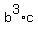 = 3993 is not divided by 5, neither "b" nor "c" are multiple of 5.
Hence, from (4), "a" is multiple of 5.
Having it, it is not difficult to conclude further that b = 11 and c = 3.
a + b + c = 5 + 11 + 3 = 19. = 3993 is not divided by 5, neither "b" nor "c" are multiple of 5.
Hence, from (4), "a" is multiple of 5.
Having it, it is not difficult to conclude further that b = 11 and c = 3.
a + b + c = 5 + 11 + 3 = 19.
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|