Question 1104191: The digits 2,4,6,8,0 are used to make five-digit numbers, with no digit repeated. What is the probability that a number chosen at random from these numbers has the property that the digits in the thousands's place and the ten's place are each larger than their neighboring digits?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! With the  digits 2,4,6,8,0, we can make digits 2,4,6,8,0, we can make
 different 5-digit sequences, with no digit repeated. different 5-digit sequences, with no digit repeated.
However,  of those sequences start with 0, of those sequences start with 0,
and should not count as 5-digit numbers.
As a consequence, there are  5-digit numbers 5-digit numbers
made with the digits 2,4,6,8,0, with no digit repeated.
A few of those have the property that
digits in the thousands's place and the ten's place
are each larger than their neighboring digits.
For that to occur,
8 must be either in the thousands's place, or the ten's place,
because otherwise it would be larger than a neighbor in one of those places.
The other digit greater than its neighbors must be either 6 or 4 due to similar reasoning.
If 8 and 6 are the greater than their neighbors digits,
either one can be in the ten's place (2 choices),
0 can be placed at the one's or hundred's place (2 choices), and then
2 and 4 can fill the other two spots in either order (2 choices).
That accounts for  numbers with the desired properties: numbers with the desired properties:
28460, 48260, 28064, 48062, 26480, 46280, 26084, 46082.
If 8 and 4 are the greater than their neighbors digits,
6 must be placed at the end next to 8, o it is not next to 4 (1 choice),
and then 2 and 0 can occupy the spots next to 4 in either order.
That accounts for  more numbers starting with 68: 68042, 68240. more numbers starting with 68: 68042, 68240.
The last choice is the  and only choice for numbers ending in 86: 24086. and only choice for numbers ending in 86: 24086.
The total count is  numbers that satisfy all the requirements numbers that satisfy all the requirements
out of the 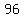 five-digit numbers, made with 2,4,6,8,0, with no digit repeated. five-digit numbers, made with 2,4,6,8,0, with no digit repeated.
The probability that one randomly chosen number
out of the 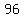 five-digit numbers, made with 2,4,6,8,0, with no digit repeated five-digit numbers, made with 2,4,6,8,0, with no digit repeated
has the property that the digits in the thousands's place and the ten's place are each larger than their neighboring digitsis
 . That is approximately . That is approximately  or or 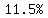 . .
|
|
|