Question 1104186: Find the sum of 1/2(4) +1/3(5) + 1/4(6) + ..... + 1/13(15)
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!
Each of the fractions is of the form  .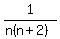
Whenever you see a problem like this, where you are adding several terms of the same form, it is almost certain that you can write each term in such a way that, when all the terms are added, most of the terms cancel, leaving you with a relatively simple answer.
So let's find a way to "decompose" the general term into the sum of two terms. Since the denominator is n(n+2), we want to write the term as the sum of two fractions, one with denominator n and the other with denominator (n+2).
This equation must be true for all values of n; that means
 and 
Solving that system of equations gives us
A = 1/2; B = -1/2
So the general term of the sequence can be written as
Now rewrite each term as the sum of two terms, using this pattern:
...
Now looking at the terms in parentheses, you see that there is a 1/4 and a -1/4, a 1/5 and a -1/5, ..., and a 1/13 and a -1/13.
So all those terms cancel; all that is left is the first fractions from the original first two terms and the second fractions from the original last two terms:
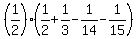
So, using a common denominator, the sum we are looking for is
Answer by ikleyn(52786)  (Show Source):
|
|
|
