Question 110414: If (2x - 1)(2 + 5x)=Ax2 + Bx + C, what is the value of B? the Ax2 means dat 2 is da power of A?
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! First thing: The Ax2 means that x, not A is raised to the second power. Actually, you should use the ^ mark (Shift-6) to indicate power, like this: Ax^2.
:
To solve this problem you need to use the FOIL process, First, Outside, Inside, Last.
:
In your problem: 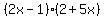 , the first thing to do is rearrange the second factor, 2+5x, so that things are in the proper order: , the first thing to do is rearrange the second factor, 2+5x, so that things are in the proper order:
:
 . .
:
Now,
:
Firsts: 2x, 5x
Outsides: 2x, 2
Insides: -1, 5x
Lasts: -1, 2
:
You need to find the product of the Firsts, PLUS the product of the Outsides, PLUS the product of the Insides, PLUS the product of the Lasts, and then collect like terms.
:


 , and finally , and finally

:
Now add them all together:
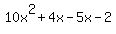 , and collect terms , and collect terms
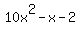 , because , because 
:
Since the coefficient on the 2nd term is -1, that is the value of B in your original problem statement.
|
|
|